We Spent All Day Arguing About This Triangle Brain Teaser. Can You Solve It?
There’s nothing quite like a maddening math problem, mind-bending optical illusion, or twisty logic puzzle to halt all productivity in the Popular Mechanics office. We’re curious people by nature, but we also collectively share a stubborn insistence that we’re right, dammit, and so we tend to throw work by the wayside whenever we come upon a problem with several seemingly possible solutions.
This triangle brain teaser isn’t new—shoutout to Popsugar for unearthing it a couple years ago—but based on some shady Internet magic, the tweet below reappeared in my feed today and kick-started a new debate on our staff-wide Slack channel, a place traditionally reserved for workshopping ideas, but instead mostly used for yelling about other stuff that we occasionally turn into content.
Say? pic.twitter.com/lrhXrWw5EP
— J (@jiteshpillaai) April 9, 2018
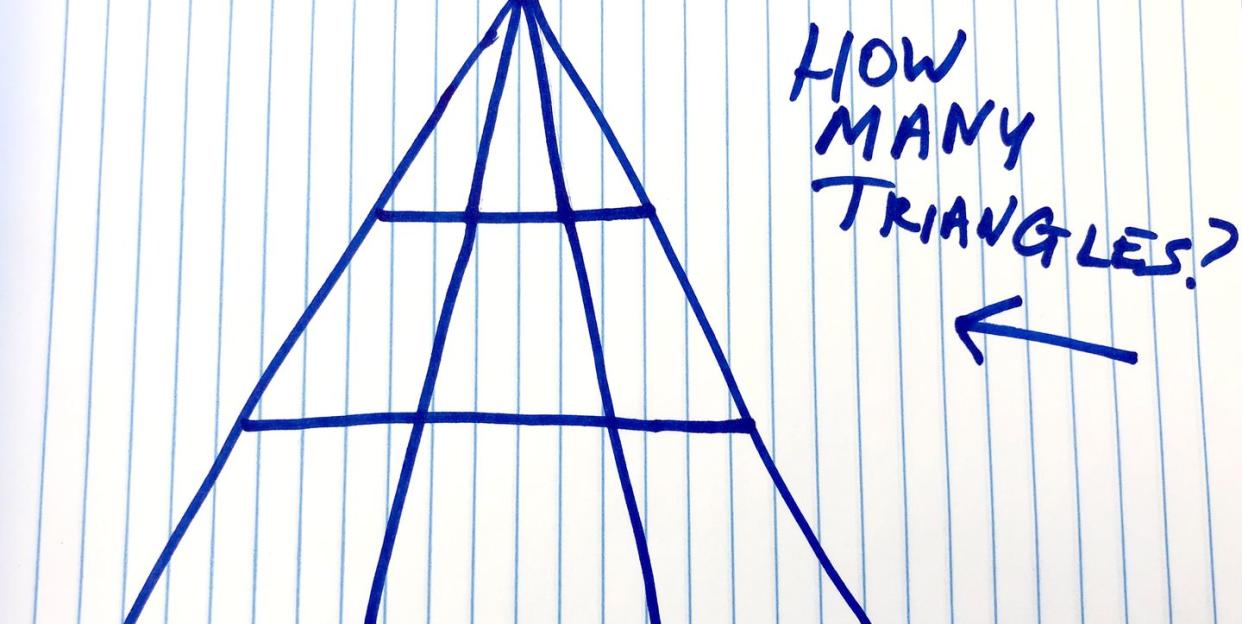
Because I’m a masochist, I drew the triangle again and asked everyone on staff to promptly drop what they were doing and attempt to solve the simple question: How many triangles can you find?
I’ll spare you the full conversation—trust me, nobody wants to see that—but the team’s responses ranged all over the place. Some editors saw four triangles. Others saw 12. A few saw 6, 16, 22. Even more saw 18. One wiseguy counted the triangles in the As in the question itself, while another seemed to be having an existential crisis: “None of these lines are truly straight, just curves—thus you cannot define any of them as a triangle,” he said. “There are no triangles in this photo. Life has no meaning.”
We then posed the problem to our Instagram followers, whose replies also ran the gamut, from 5 to 14 to 37. While we acknowledge the high probability of trolling here, it’s clear that people respond to the problem many different ways.
A post shared by Popular Mechanics Magazine (@popularmechanics) on Jan 29, 2020 at 12:14pm PST
I could’ve listened to my colleagues explain their questionable processes all day, but instead, I reached out to several geometry experts to see if we could arrive at a consensus answer. Turns out virtually all of the mathematicians I contacted found the same solution—but not all of them figured it out in the same way.
If you don’t want to know the answer just yet, stop reading and try to solve the problem first. I’ll meet you back here when you’re done.
Hey, that was quick. Ready for the answer? Unlike some viral math problems that are purposely vague and open for interpretation, this one actually does have a slam-dunk, no-doubt-about-it solution, and it’s 18. Let’s hear from some of the geometry experts as to why.
“I would approach this just like one approaches any mathematical problem: reduce it and find structure,” says Sylvester Eriksson-Bique, Ph.D., a postdoctoral fellow with the University of California Los Angeles’s math department.
The only way to form triangles in the figure I drew, Erikkson-Bisque says, is if the top vertex (corner) is part of the triangle. The base of the triangle will then have to be one of the three levels below. “There are three levels, and on each you can choose a base among six different ways. This gives 18, or 3 times 6 triangles.”
Let’s look at the master triangle again.

“It’s convenient to generalize to the case where there are n lines passing through the top vertex, and p horizontal lines,” says Francis Bonahon, Ph.D., a professor of mathematics at the University of Southern California.
In our case, n = 4, and p = 3. Any triangle we find in the drawing should have one top vertex and two others on the same horizontal line, so for each horizontal line, the number of triangles with two vertices on that line is equal to the number of ways we can choose these vertices, Bonahon says—namely the number of ways we can choose two distinct points out of n, or “n choose 2.”
Remember high school math? That’s n(n-1)/2. And since there are p horizontal lines, says Bonahan, this gives p n(n-1)/2 possible triangles. In our case, that’s 3x4(4-1)/ 2=18.
Here’s a handy breakdown of how to find each possible triangle:

Johanna Mangahas, Ph.D., an assistant math professor at the University at Buffalo, also came to 18—first through simple brute-force counting, then through the same crafty combinatorics as above—but admits our triangle brain teaser isn’t quite as cool as this one from Po-Shen Loh, Ph.D., a math professor at Carnegie Mellon University in Pittsburgh, as featured in the New York Times last year:

This one has a slicker mathematical answer, she says, because here, counting triangles is the same thing as counting combinations of three lines chosen out of six [6-choose-3 = (6*5*4)/(3*2*1)].
“In that case, every pair of lines intersects and there are no triple-or-more intersections, so any choice of three always gives a triangle,” says Mangahas. In the picture I sent her, some lines are parallel, so they can’t be part of the same triangle. “If you took the same seven lines and shook them up a bit, probabilistically they’d most likely land like [Loh’s] problem and you’d have more triangles and a similar cute answer.” (For the record: 35.)
Whew. I haven’t shared this new triangle problem with my coworkers yet. But it’s only a matter of time before they discover it—and argue some more.
🚨IMPORTANT UPDATE 1/30/20🚨: Since publishing this story, many, many readers have reached out to let me know that while 18 is indeed an acceptable answer to this problem, it isn’t the only one, due to some unintentional oversight on my part. I could have made this much easier on readers—and, crucially, much easier on my inbox—had I just sketched the triangle on plain, white computer paper. But no.
I unfortunately drew this triangle on lined paper, and lots of smart people have correctly pointed out that, well, actually, if you count the light blue parallel lines in the image in addition to the dark blue lines written in marker, there are actually more than 18 total triangles here—considerably more. I never specified to only use those dark blue lines, and thus, I am wrong. You are right.
One reader, Ralph Linsangan, totally owned me by sending this image, in which he marks every additional triangle found under the technicality, flagging 17 additional triangles for a total of 35. Behold:

That kind of dedication is just one of many reasons I love Popular Mechanics readers. We can’t get anything past you guys. Until the next teaser!
🚨YET ANOTHER TRIANGLE UPDATE 1/31/20🚨: Since posting the last update, I’ve heard from even more of you, continuing to chide me—and your fellow readers—for not considering additional possible triangles. Let’s hear from reader Derek Schneider, who sent in another graphic suggesting there are 45 triangles.
If we follow the original rules however, I count and additional 9 that are definite (in green) and one that could be open to interpretation depending on how you visually place the top vertex (in purple)…I would personally count it.

Reader Poingly, meanwhile, wrote in to say we’ve been making a “grave error” in counting the triangles all along:
Take the bottom right corner, for instance, it shows one arrow for one triangle. However, these light blue lines could conceivably form as many as THREE triangles in this one corner alone:

While some of these MAY be somewhat debatable (ie, where EXACTLY do the light blue lines intersect the dark ones and do they technically form a triangle or a quadrilateral), I have counted SEVEN ADDITIONAL triangles that may be made in this way. This bring the total number of triangles up to 42.
The bad news is that we missed some triangles. The good news is that this confirms that life clearly DOES have meaning, as evidenced by the exact number: 42.
Outstanding point, Poingly. Reader James Goodrich took it another step further, suggesting we open our minds to consider what a triangle could be:
Well, according to your reader, who pointed out 17 additional triangles (using the "Andrew didn't specify what lines can comprise the 3 edges of a triangle" clause), failed to clearly find quite a lot more. Take, for example, the bottom-left mini-triangle in the 30 Jan 2020 "Important Update" addendum. Would not the areas of the mini-triangle and the area of the rhombus adjacent to it, combined, make for another triangle?
Another idea for consideration: Triangles have 3 angles (who would have guessed?); however, I would postulate that how you describe a triangle, by way of said angles, would generate different triangles. Given a triangle T, with vertices A, B, and C, t-one might indeed be described by ABC, with B being the central angle. I suggest that t-two, being described by BAC, is different. Similarly for BCA.
If we then take a particular case, right-angle triangles, we can derive sine, cosine, and tangent functions (SOH, CAH, TOA). If we were to apply that to the triangle (and relax the right-angle requirement, it might mean that BAC is different than CAB. Of course, exceptions are made for isoscolese and equilateral triangles (the latter would only have 3 distinct triangle definitions).
I haven't quite thought of how to quantify each suggestion (and applying the latter after the former would increase the count still), so I don't have an easy number for you to use in an updated important update (if you found my ideas worthwhile to update).
I did, James. And I’ll be waiting. Begrudgingly, I decided to take one last stab at figuring out just how many additional triangles there could be given our new chaotic rules, and arrived at 43, for a total of 61:

I’m quite sure, however, that someone reading this will very quickly tell me I’m wrong yet again and deliver proof of even more hidden triangles, sending me down another rabbit hole on the long and winding path to eventual insanity. (Side note: I haven’t seen my wife in three days. Please tell her I love her.) So I’m issuing one last challenge: If you can find the most possible triangles in the original image, show me your work, and definitively prove your supremacy, I will update this story one final time and crown you the Triangle King or Queen, now and forever. Godspeed.
You Might Also Like

