Is It Quantum Computing or Not?
This week I had a fascinating discussion on BBC Radio 4 with Dr Geordie Rose, the CTO of DWave, triggered by the news that NASA and Google are investing in DWave's "quantum computer". The idea is to set up a facility that is used by both NASA and Google but also allows academics to book time on the system to try out new ideas.
Our radio conversation brought out an important issue that has dogged this subject for several years: when is a quantum computer not a quantum computer?
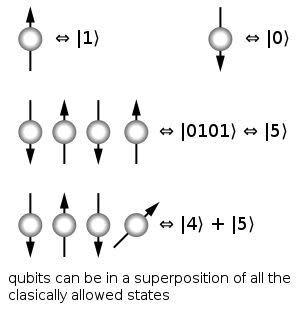
I began by explaining the theory behind quantum computing and why they hold the promise of significantly faster processing. In essence, it relies upon the fact that whilst conventional "bits" can be 0 or 1, quantum bits (so called qubits) can be both 0 and 1 at the same time (known as superposition). If you can combine qubits (known as entanglement) you can have a system that can process values that expand exponentially with the number of qubits you entangle. As with conventional programming, these qubits are passed through various logic gates to achieve the desired results. Hence, this is known as the "gate theory" of quantum computing.
Many academics, and increasingly large corporations such as IBM and Microsoft, have spent years working on the algorithms, error correction and a variety of techniques for creating qubits, ranging from photons to ion traps to braided anyons. To date, we have found it extremely difficult to maintain these qubits in superposition and to ensure they are truly entangled. "Decoherence", where the qubits drop out of superposition and become just a 0 or a 1, is the bane of all quantum computer engineers.
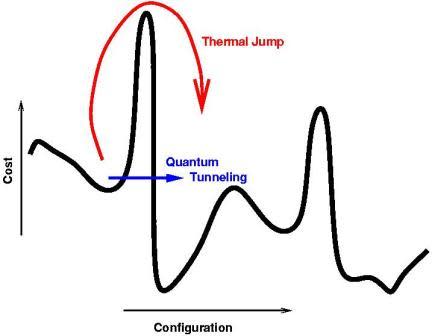
This decoherence problem has spurred many to look for methods that are naturally immune from the effect. DWave were one such group. They have based their processor on an effect called quantum annealing, also sometimes referred to as adiabatic quantum computing, which was first discussed in 2000 as a possible means of conducting certain calculations.
The quantum annealing process is, as the name suggests, a quantum level effect. At the scale of a qubit, you can use the effect to determine the lowest "energy" state of a system. Hence, if you can describe a problem in terms of a function that has a "cost" of "energy" versus some other parameter, you can find the configuration that represents the optimal state. So, for example, think of the classic travelling salesman problem where one tries to find the shortest path when travelling between a number of cities. If you did this using simple trial and error on a conventional computer it would take longer than the age of the universe by the time you were up to 30 cities. Using quantum annealing you can define the problem as an optimisation task which means you can programme a DWave system to calculate it.
An obvious question is how much faster is quantum annealing than conventional computers? Based upon solving specific problems, that question was addressed in a paper just published, where academics compared conventional computers with a DWave system when solving optimisation problems which were known to be computationally hard. The DWave system is reported as being many thousands of times faster in some cases.
Thus, we have a system that can do useful computations based on quantum effects. It may not be a quantum computer as some purists might define it, but it does have one huge advantage: it exists and is available to do meaningful work. For all the theory, quantum computers based upon gate theory are still very experimental and can muster only a handful of qubits. Gate based quantum computing will come eventually; the money being invested and the screaming need for the technology as we head towards the end of Moore's law mean that it's a question of when not if. But, on the journey, which is currently of uncertain length, we should not be blind to opportunities on the way. It may prove to be a detour, but many interesting developments have arisen in computing by those who spotted just such an opportunity.
So, is DWave's system a quantum computer? I think that's the wrong question. Better to ask if the DWave system can help with some computations that were previously impractical, in which case the answer is yes.
Images:
D-Wave Systems, Inc., Arnab Das, WhiteTimberwolf, Saurabh.harsh
Follow Scientific American on Twitter @SciAm and @SciamBlogs. Visit ScientificAmerican.com for the latest in science, health and technology news.
© 2013 ScientificAmerican.com. All rights reserved.